今天重温了关于Attention Mechanism的名篇 Attention is all you need,奈何原文实在是有些晦涩,最终还是转向了前辈们的review。Illustrated Transformer 是其中比较著名的一篇博文,中译版 请戳这里。本文主要记录我对self-attention机制的一些思考。
如何理解
其实attention本身只是人看到一个场景时的本能反应,即我们会更加关注场景中的一些特定区域。机器学习领域的自注意力机制更像是对这种现象的一种抽象。这种思想应用在算法和模型上就会转化为correlation或similarity的评估,最终表现为不同components间的weights。对于一个句子,这个weights就会是字与字间的相关性;对于一张图片,这个weights就会体现像素与像素间的依赖性。
博文中的应用场景主要是机器翻译,作者举了一个很好的例子:“The animal didn’t cross the street because it was too tired” 这句话中的 “it” 指代的是什么呢?对于语言模型来说,这个问题并不像人类理解这个句子一样简单。

如果我们在这个问题上应用self-attention,那么此处的 “it” 与句中其他词的联系就可以帮我们找到答案。对于机器翻译的场景,这些联系就可以作为模型翻译当前词汇的线索,从而更加精确地理解和编码当前词。同样地,如果我们在语义分割的场景下应用 self-attention,那么当前像素与周边像素的相似性信息就可以帮助我们更好地确定当前像素所属的class。
如何计算 (以机器翻译为例)
单步计算
(1) Word to Embedding-vec
通过embedding将每个输入词汇转化为表征向量 \(X_i\)
(2) 生成 query, key, value 向量
使用 \(W^Q\), \(W^K\), \(W^V\) 三个转换矩阵为每个向量 \(X_i\) 生成对应的 query vector \(q_i\), key vector \(k_i\), value vector \(v_i\)
(注意: 此处的转换矩阵需要在训练过程中学习,且由所有表征向量共享) 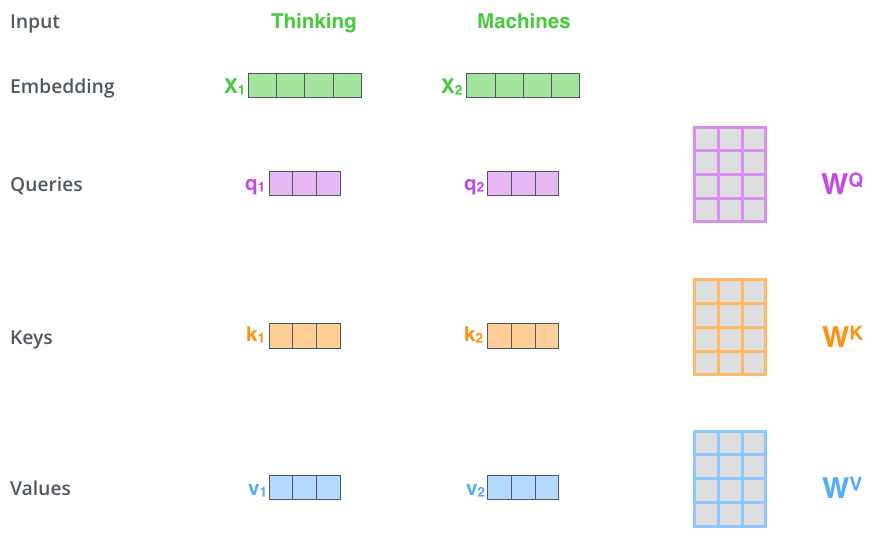
(3) 计算 attention 分值
编码每个词向量 \(X_i\),我们需要评估它和所有其他词向量相关性。对于一个其他词向量 \(X_j\),他们的相似度 \(S_i\) 可以通过点积得到: \[\begin{align*}
Similarity(X_i, X_j) = q_i \cdot k_j
\end{align*}\]
(4) 稳定梯度 & 归一化
我们对所有相似度除以 \(\sqrt{dim(key)}\) 来稳定梯度,并使用softmax来对所有以当前词为主体的相似性评估进行归一化操作。
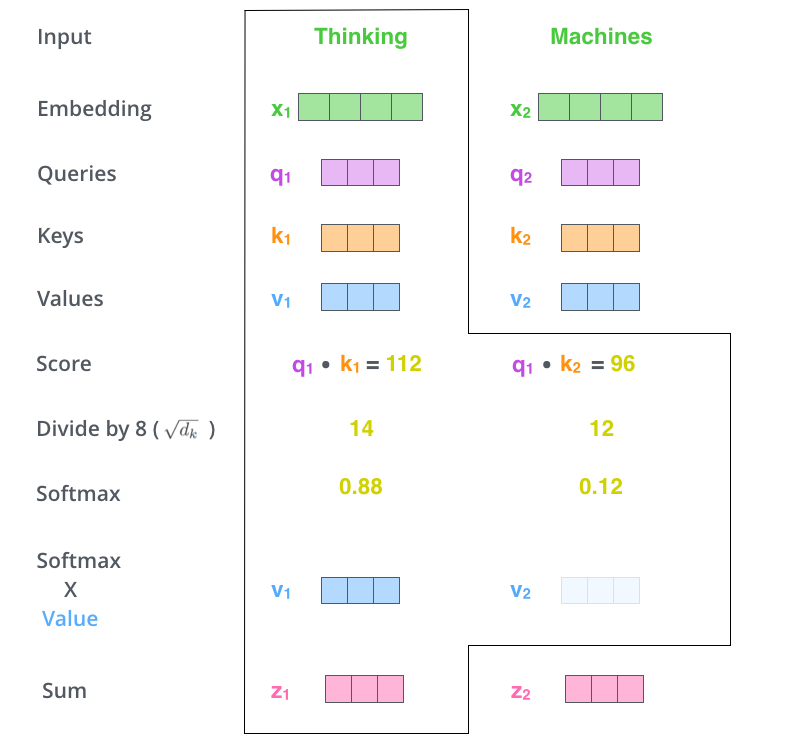
(5) 加权 Self-attention Value
我们使用相似度 \(S_j\) 来调整 \(v_j\) 的大小,并加权得到最终的Self-attention评分: \[\begin{align*}
z_i &= \sum_j S_j \cdot v_j
\end{align*}\]
矩阵计算
在实际计算中,上述的self-attention是通过矩阵操作来进行计算的:
1. 计算所有词向量的 query, key, value 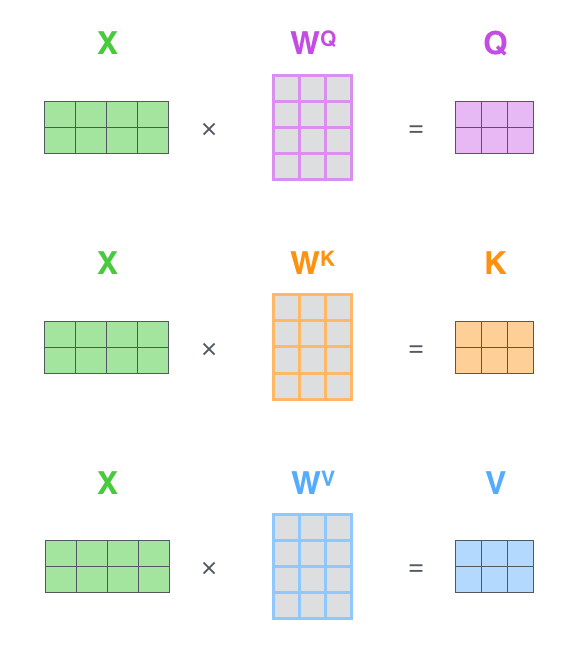
2. 计算 Self-attention 评分 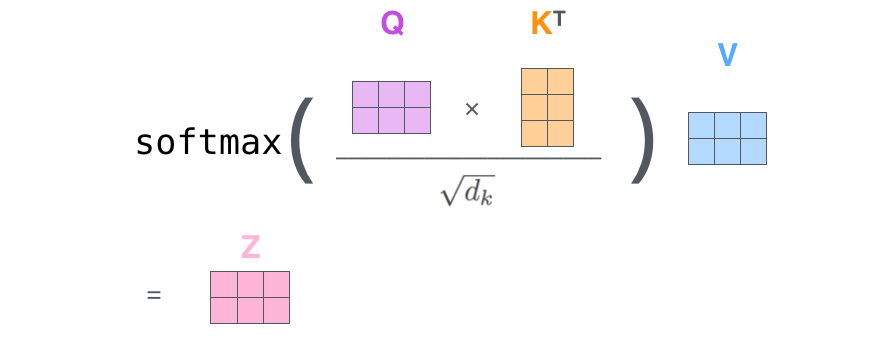
多头机制
在实际应用中,多头机制(multi-headed)经常被应用于self-attention,即存在多组转换矩阵 \(W^Q\), \(W^K\), \(W^V\) 来增加模型关注于不同位置的能力、赋予attention更丰富的子表达方式。多组 \(Z\) 矩阵会通过另一个可训练的转换矩阵 \(W^O\) 变换成符合前向网络input size的矩阵。 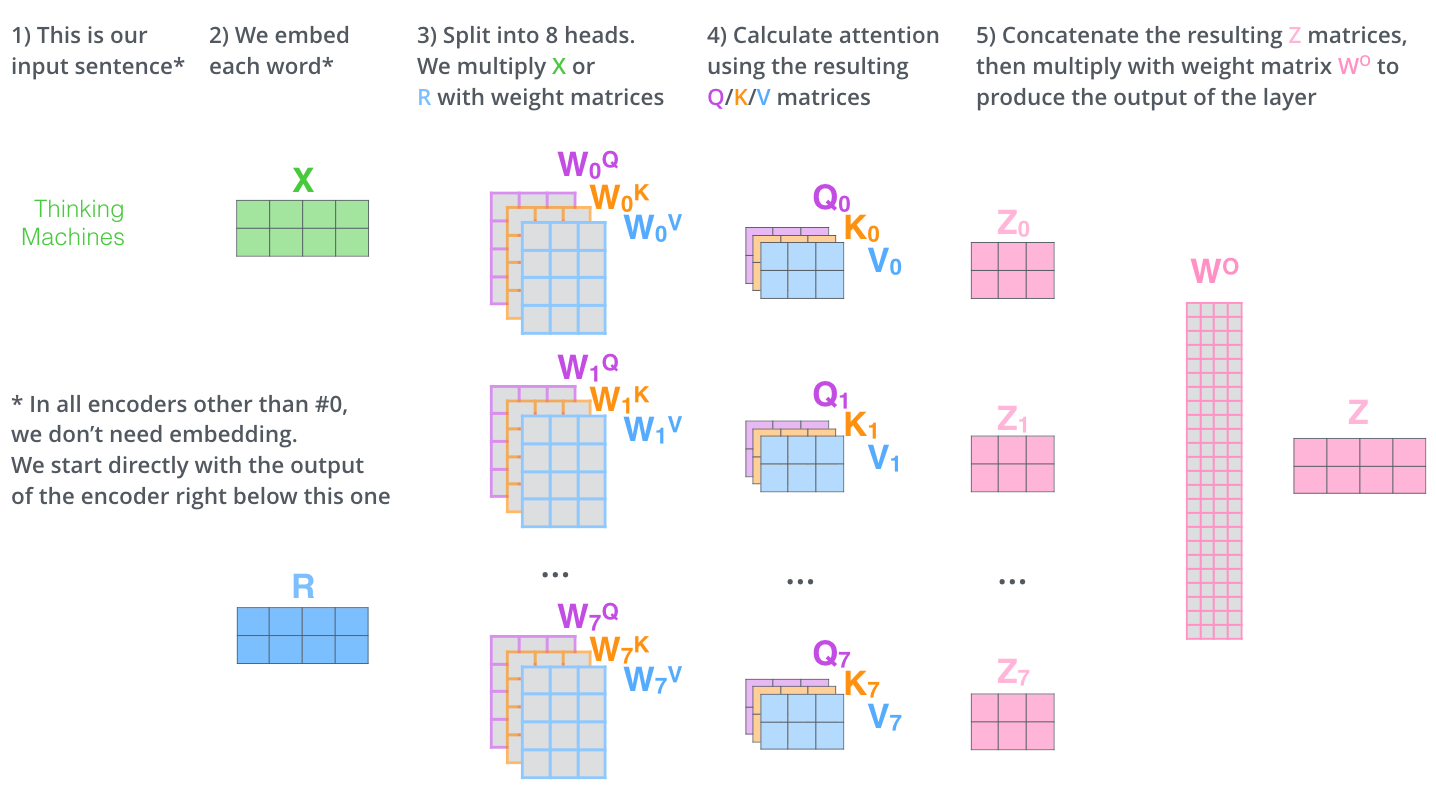
Self-attention for SSEG
应用于语义分割场景的Self-attention (待补充...)